In my last post, I showed you how you could use a number of SQL tricks to generate a class of fractals known as the “escape-time fractals”. In this post I’ll show you how you can use the same tricks to generate a completely different set of fractals known as the “self-similar fractals”.
Self-similar fractals are based on the idea of having an initial pattern and some rule for generating the next iteration of that pattern. One of the classic self-similar fractals is the Heighway dragon:
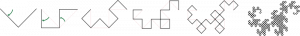
To generate the curve, you first start with a single line segment. To generate the next iteration of the Heighway drag, you “bend” each line segment of the curve in half. If you apply this to the initial line segment, you get a curve shaped like a “v”. If you apply it to the v-shaped curve, you get a curve shaped like a C clamp. If you keep repeating this, you eventually get the curve on the far right of the image above.
Given this definition of the Heighway dragon, it’s unclear how we might go approach implementing it. Fortunately, there is a convenient way of describing self-similar fractals known as “L-systems“.
L-Systems
L-systems are ultimately a way of encoding self-similar fractals as strings. The idea is you have an initial string which encodes the path to generate the initial version of the fractal. You then have a set of string replacement rules that when applied to the string give you a string representing the next iteration of the fractal. For the Heighway dragon, the L-system looks something like this:
Initial String: FX Replacement Rules: X -> X+FY+ Y -> -FX-Y
The rule “X -> X+YF+” means you replace all “X”s in the current string with the string “X+YF+”. When you run this L-system, you get a sequence of strings, each describing one iteration of the Heighway dragon:
FX FX+YF+ FX+YF++-FX-YF+ FX+YF++-FX-YF++-FX+YF+--FX-YF+
To decode one of these strings into the curve, you interpret all “F”s as moving forward one unit, interpret all “+”s as turning right, interpret all “-“s as turning left, and interpret all other characters as doing nothing. Based on this decoding, we can interpret the initial string “FX” as a a single step forward. In other words, a single line segment. The string “FX+YF+” represents a step forward, a turn to the right, and another step forward, and a turn to the right. This gives us a “v” shape curve. These are exactly the first two iterations of the Heighway dragon. You may want to play with the L-system yourself for a bit, but you should be able to convince yourself it generates the curve. This gives us some hope that it’s possible to implement a SQL query to generate the Heighway dragon.
Writing the SQL Query
(If you don’t care about the specifics of how this is mapped to a SQL query, you can skip this section.)
Now that we’ve got a sense of an approach we can use to generate the Heighway dragon, let’s start thinking about how we can turn this into a SQL query. We can implement the Heighway dragon with a three part SQL query:
- First, we run the L-system. We use a recursive CTE to generate the Nth string in the L-system.
- We convert the L-system string to a set of line segments. We do this by having a recursive CTE iterate through the L-system string and have it trace the path described by the string.
- We convert the line segments into the fractal. We do this by using the same approach we used last time. We can produce an MxN grid of points, iterate through every point, and check whether or not each point describes a point on the curve. When then combine all the points together to produce the final fractal.
Running the L-system
Running the L-system winds up being the easiest part. The description of an L-systems maps directly to a recursive CTE. We start with an initial string and run some string replacements to produce the next iteration of the L-system. We keep doing this for some fixed number of iterations. We can do this with the following SQL query:
WITH RECURSIVE iterations AS (
SELECT 'FX' AS path, 0 AS iteration
UNION ALL
SELECT replace(replace(replace(PATH, 'X', 'X+ZF+'),
'Y', '-FX-Y'),
'Z', 'Y') AS PATH,
iteration + 1 FROM iterations
WHERE iteration < 8
) SELECT * FROM iterations;
path | iteration
--------------------------------+-----------
FX | 0
FX+YF+ | 1
FX+YF++-FX-YF+ | 2
FX+YF++-FX-YF++-FX+YF+--FX-YF+ | 3
...
(We need to use slightly different replacement rules where we replace “X” with “X+ZF+” and then later replace “Z” with “Y“. This is so any “Y”s created by the “X” substition rule aren’t immediately modified by the “Y” substitution rule.)
The query starts with the initial string “FX“. It does the substitutions described by the L-system a total of eight times. This gives us the L-system string for the first eight iterations of the curve.
Generating the Line Segments
Converting the L-system string to a list of line segments is the most involved part of the SQL query. We start by having a recursive CTE iterate through the characters of the string returned by the last iteration of the previous query. As we iterate through the string, we can maintain:
- The rest of the path we need to traverse.
- The start, mid, and endpoint of the previous line segment. Each of these can be encoded as a row value and a column value.
- The current direction we are heading in. We can encode this as two values, row_diff and col_diff, that describe what would happen if we were to take a step. row_diff describes how the current row would change and col_diff describes how the column would change. For example, if we are facing to the left, the column value would be -1 (move towards the decreasing column), while the row value would be 0 (don’t change the row we are in)
As we iterate through the string, there are three different cases we need to handle:
- When we see a “+” or “-“.
- When we see an “F”.
- When we see any other character.
When we see a “+” or “-“ the only thing that needs to change is the current direction. Depending on which direction we are turning, we can perform the following updates1:
# Moving to the right: row_diff = col_diff col_diff = -row_diff # Moving to the left: row_diff = col_diff col_diff = -row_diff # Any other case: row_diff = row_diff col_diff = col_diff
To handle the case where we see an “F”, we can calculate a value step_size. Whenever we see an “F”, we set it to 1, otherwise we set it to 0. We can then calculate the end point of the next line segment based on the end point of the previous line segment, the current direction we are facing, and the value of step_size. Using step_size ensures we only take a step forward when we see an “F”.
Based on the above updates, we automatically handle the case where we see any other another character. The direction we are heading in remains the same and we take a step of size zero which means our position doesn’t change.
We can implement all of this in a recursive CTE that looks like the following:
segments AS (
SELECT
0 AS start_row,
0 AS start_col,
0 AS mid_row,
0 AS mid_col,
0 AS end_row,
0 AS end_col,
0 AS row_diff,
1 AS col_diff,
(SELECT path FROM iterations ORDER BY iteration DESC LIMIT 1) AS path_left
UNION ALL
SELECT
end_row AS start_row,
end_col AS start_col,
end_row + row_diff * step_size AS mid_row,
end_col + col_diff * step_size AS mid_col,
end_row + 2 * row_diff * step_size AS end_row,
end_col + 2 * col_diff * step_size AS end_col,
CASE WHEN SUBSTRING(path_left FOR 1) = '-' THEN -col_diff
WHEN SUBSTRING(path_left FOR 1) = '+' THEN col_diff
ELSE row_diff
END AS row_diff,
CASE WHEN SUBSTRING(path_left FOR 1) = '-' THEN row_diff
WHEN SUBSTRING(path_left FOR 1) = '+' THEN -row_diff
ELSE col_diff
END AS col_diff,
SUBSTRING(path_left FROM 2) AS path_left
FROM segments,
LATERAL (SELECT CASE WHEN SUBSTRING(path_left FOR 1) = 'F' THEN 1 ELSE 0 END AS step_size) sub
WHERE CHAR_LENGTH(path_left) > 0
) SELECT * FROM segments;
Pulling it All Together
Now that we’ve got the line segments for the fractal, the last step is to convert those line segments into the fractal itself. As I mentioned before we can use a similar approach to what we did in the last post. We can do a three step process to convert the line segments into an image:
- Determine the size of the grid. This can be determined by looking at the smallest and largest x and y coordinates of any point in the fractal.
- Assign a character to each point. We can assign characters based on the following rules:
- ‘*’ – An end point of a line segment.
- ‘|’ – The midpoint of a vertical line segment.
- ‘-‘ – The midpoint of a horizontal line segment.
- ‘ ‘ – Any point that’s not part of the fractal.
- Combine all the characters together to produce the final image.
This is all done by the following query:
end_points AS (
SELECT start_row AS r, start_col AS c FROM segments UNION SELECT end_row AS r, end_col AS c FROM segments
), points AS (
SELECT r, c FROM generate_series((SELECT MIN(r) FROM end_points), (SELECT MAX(r) FROM end_points)) a(r)
CROSS JOIN generate_series((SELECT MIN(c) FROM end_points), (SELECT MAX(c) FROM end_points)) b(c)
), marked_points AS (
SELECT r, c, (CASE WHEN
EXISTS (SELECT 1 FROM end_points e WHERE p.r = e.r AND p.c = e.c)
THEN '*'
WHEN EXISTS (SELECT 1 FROM segments s WHERE p.r = s.mid_row AND p.c = s.mid_col AND col_diff != 0)
THEN '-'
WHEN EXISTS (SELECT 1 FROM segments s WHERE p.r = s.mid_row AND p.c = s.mid_col AND row_diff != 0)
THEN '|'
ELSE ' '
END
) AS marker
FROM points p
), lines AS (
SELECT r, string_agg(marker, '') AS row_text
FROM marked_points
GROUP BY r
ORDER BY r DESC
) SELECT string_agg(row_text, E'\n') FROM lines;
Producing Fractals
After all that, we wind up with this one giant 61 line SQL query that generates the Heighway dragon:
WITH RECURSIVE iterations AS (
SELECT 'FX' AS PATH, 0 AS iteration
UNION ALL
SELECT replace(replace(replace(PATH, 'X', 'X+ZF+'), 'Y', '-FX-Y'), 'Z', 'Y'), iteration+1 AS iteration
FROM iterations WHERE iteration < 8
), segments AS (
SELECT
0 AS start_row,
0 AS start_col,
0 AS mid_row,
0 AS mid_col,
0 AS end_row,
0 AS end_col,
0 AS row_diff,
1 AS col_diff,
(SELECT path FROM iterations ORDER BY iteration DESC LIMIT 1) AS path_left
UNION ALL
SELECT
end_row AS start_row,
end_col AS start_col,
end_row + row_diff * step_size AS mid_row,
end_col + col_diff * step_size AS mid_col,
end_row + 2 * row_diff * step_size AS end_row,
end_col + 2 * col_diff * step_size AS end_col,
CASE WHEN SUBSTRING(path_left FOR 1) = '-' THEN -col_diff
WHEN SUBSTRING(path_left FOR 1) = '+' THEN col_diff
ELSE row_diff
END AS row_diff,
CASE WHEN SUBSTRING(path_left FOR 1) = '-' THEN row_diff
WHEN SUBSTRING(path_left FOR 1) = '+' THEN -row_diff
ELSE col_diff
END AS col_diff,
SUBSTRING(path_left FROM 2) AS path_left
FROM segments, LATERAL (SELECT CASE WHEN SUBSTRING(path_left FOR 1) = 'F' THEN 1 ELSE 0 END AS step_size) sub
WHERE CHAR_LENGTH(path_left) > 0
), end_points AS (
SELECT start_row AS r, start_col AS c FROM segments UNION SELECT end_row AS r, end_col AS c FROM segments
), points AS (
SELECT r, c FROM generate_series((SELECT MIN(r) FROM end_points), (SELECT MAX(r) FROM end_points)) a(r)
CROSS JOIN generate_series((SELECT MIN(c) FROM end_points), (SELECT MAX(c) FROM end_points)) b(c)
), marked_points AS (
SELECT r, c, (CASE WHEN
EXISTS (SELECT 1 FROM end_points e WHERE p.r = e.r AND p.c = e.c)
THEN '*'
WHEN EXISTS (SELECT 1 FROM segments s WHERE p.r = s.mid_row AND p.c = s.mid_col AND col_diff != 0)
THEN '-'
WHEN EXISTS (SELECT 1 FROM segments s WHERE p.r = s.mid_row AND p.c = s.mid_col AND row_diff != 0)
THEN '|'
ELSE ' '
END
) AS marker
FROM points p
), lines AS (
SELECT r, string_agg(marker, '') AS row_text
FROM marked_points
GROUP BY r
ORDER BY r DESC
) SELECT string_agg(row_text, E'\n') FROM lines;

Now for the really cool thing. We wrote our query to take the L-system for the Heighway dragon and produced the fractal for it. Since we didn’t make any other assumptions about the Heighway dragon, we can replace the L-system for the Heighway dragon with any L-system we want! For example, another well known self-similar fractal is the Hilbert curve:

The Hilbert curve starts by taking an initial u-shaped curve that starts in the bottom left and ends in the bottom right. You can connect four of these curves together to produce a larger curve that starts in the bottom left and ends in the bottom right. You can repeat this process to produce the next iteration of the curve. The L-system for the Hilbert curve is as follows:
Initial String: A Replacement Rules: A -> -BF+AFA+FB- B -> +AF-BFB-FA+
We can modify our query above to use this new L-system:
SELECT 'A' AS PATH, 0 AS iteration
UNION ALL
SELECT replace(replace(replace(PATH, 'A', '-CF+AFA+FC-'), 'B', '+AF-BFB-FA+'), 'C', 'B'),
iteration + 1
FROM iterations
WHERE iteration < 4
And we now get a query that produces the Hilbert curve:
This means we can use this query to produce any self-similar fractal that can be described by an L-system! We just plug in the L-system we want and get back a query that produces the fractal!
- If you’re familiar with linear algebra, these operations correspond to the matrices for rotating by 90°.